fcBGA-H封装瞬态热特性 仿真&测试
日期:2019-02-27
1. 简介
Flip-chip(倒装芯片)封装广泛应用于桌面计算机、服务器和各种通讯设备。随着功能要求的提高,功率和热流密度越来越大。因此,对于高功率倒装芯片,客户在不断的推进TIM(热界面材料)的低热阻化。
TIMs(Thermal Interface Materials)是用于提高固体接触面之间传热性能的导热材料。比如CPUs和散热器之间,若出现微小间隙,由于空气导热性能极差,整个散热效率就会严重降低。因此,TIM的热特性对于散热方案的可靠性是至关重要的,尤其是发热部位的最高温度(结温Tj),散热片上表面温度(壳温Tc),和上述两点之间的热阻。测壳温Tc的传统方法是,在散热片中心放置一个热电偶。该方法的一个最大问题是只能用散热片中心位置的温度来表征壳温。但是在实际应用中,最高温度的位置我们通常不确定,尤其是当给结区加载非均匀热载荷(non-uniform power)的时候。
本文主要讨论的是:
a. 描述如何使用不借助热电偶的瞬态测试设备测试fcBGA封装器件(由STATS ChipPAC制造)的TIM热特性,尤其是结壳热阻Rjc;
b. 描述如何测试在风扇不同转速下(模拟真实工况)封装器件的Rja(结到环境的热阻);
c. 阐明功率脉普对结构函数的影响;
d. 描述如何通过仿真生成一个仿真结构函数,再用测试结构函数来修正仿真结构函数,最后用修正后的结构函数生成热阻网络模型,应用于系统级产品中;
e. 明确并改进更好的仿真和测试方法。
2. 封装器件和热测试装置的结构
STATS ChipPAC内部搭建了一个flip-chip测试装置(test vehicle),专门用于评估TIM的热特性,其结构如图1所示。待测封装器件包含如下结构,从上到下依次是:25x25x1 mm的铜制散热片,TIM层、硅芯片、底部填充层(a layer of underfill)以及焊接凸点(solder bumps)、12层总厚度为1.65mm的衬底、焊球、和PCB板。在四周,使用环氧树脂材料将铜盖和衬底粘合在一起。
.png)
图1测试装置图
在结区涂TIM的时候,控制其范围要非常小心,且厚度被严格控制在38μm,误差不能超过2μm,如图2和图3所示。厚度通过在固化过程中涂了TIM之后,在散热片上部加载机械下压力来控制。
.png)
图2 TIM覆盖范围
.png)
图3 TIM厚度测量
2.1 热测试芯片(Thermal Test Die)
现在Thermal test dies广泛应用于封装器件设计认证。图4展示了本次测试使用到的thermal test die,尺寸是10x10 mm。该芯片有4x4=16个单元,每个单元可以独立工作,也可以通过某些关联一起工作,比如均匀加热或非均匀加热。在芯片上分布有10个二极管传感器,可以用于测量中心位置、边上位置或者角落位置的温度。在本次测试中,所有16个单元都是均匀发热状态。
.png)
图4 Thermal test die
如图5所示,每一排的电阻器连接在一起,不同排之间的电阻器也联结在一起以保证同时加热整个结区,可以是并联或者串联的形式。区别在于串联能保证电阻器具有相同的电流,而并联则很难保证不同排电阻的电流强度,特别是当电流路径长度不同的时候。所以,还是采用串联比较好。
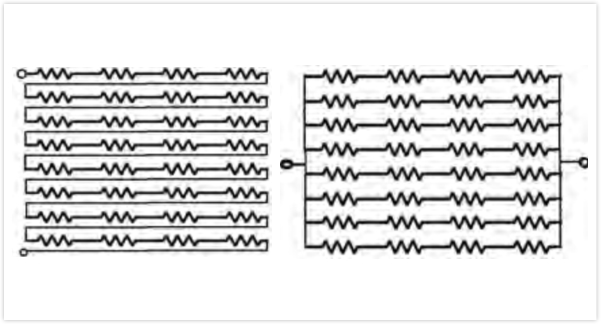
图5串联&并联加热电阻
2.2 二极管校准(标定k系数)
正如图4所示,10个二极管被置于硅芯片(silicon die)上,二极管用于测试该点的温度值。当给二极管通一小电流时,二极管两端的压降与温度呈线性关系。因此,在加热器件之前,需要先确定二极管压降和温度之间的函数关系,或称之为热敏参数。图6所示为标定该线性关系的实例。
.png)
图6 热敏感性(K系数) k = -1.755 mV/K
本次试验中,测试电流大约为5 mA,测试电压约为0.8 V,则一个二极管产生的焦耳热大约为4mW。假设结到环境的热阻为0.5 K/W,则该功率对升温的影响为
0.5 K/W x 4 mW = 0.002 ℃
可见该温升微乎其微,在大部分实际应用中均可忽略,这就保证了该测试方法的精度。
3. 测试设置
瞬态热测试装置如图7所示,我们采用成熟的商业测试系统T3Ster来分析设备的结构并测量待测器件的瞬态温度响应。
.png)
图7.测试设备
样品置于一块液冷板上方,压紧力固定为3 bar,每个样品均施加325mA的固定加热电流,即大约26 W的功率加热。当设备达到热稳态的时候,把加热电流快速切换为测试电流并在这一过程中测试二极管压降。测试之前的加热时间至少持续480 s,然后再用480 s来捕捉冷却曲线,直到设备达到新的热稳态。
每个样品需要进行两次测试:一次在盖子和冷板之间涂上导热胶,另一次不涂。每次测试都采用NID方法转化为结构函数,且相应的测量值都能互相对比。基于此,我们便能采用一种近似于JEDEC JESD 51-14标准的方法来获取样品的Rjc(结壳热阻)。
4. Rjc仿真和测试
现如今热仿真软件已经广泛应用于IC封装器件热特性的预测。研发早期的热模拟有助于预测IC封装器件的热可靠性,还能给系统级热评估和优化提供重要参数。在很多情况下,热仿真甚至代替了耗时耗力的试验。本节中,我们将对flip-chip器件的重要参数结壳热阻Rjc进行纯数值研究。不过首先,我们先对比几种不同模型下的Rjc。
4.1 固定Rjc和浮动Rjc
建立一个简单的模型来研究不同边界条件的影响。固定Rjc模型,即在盖子(lid)的上表面设定一个定温边界,如图8所示。这种情况下,向盖子上表面方向的热传递只能是垂直或者出平面方向,而盖子平面上的热扩散很少。而浮动Rjc模型,则盖子上表面温度取决于冷板工况。温度计算由如下公式描述
Rjc = (Tj - Tc)/ Power
式中,Tc为散热片上表面中心的温度。
对于浮动Rjc模型,我们考虑两种方案。一种是采用内充冷水的冷板;另一种是用一块尺寸与冷板相同且上表面恒温的铜块。三种模型的边界条件设置如图8所示,通过CFD仿真计算可以得出所有方案的Rjc。
.png)
图8.Rjc模型的边界条件 — 定温&冷板&铜块
图9展示了三个模型的温度场仿真结果。
.png)
图9.结和壳附近区域的温度分布
表1则是由此计算所得的Rjc数据。可以看出,定温边界方案的结果要比冷板和铜块的高15~20%。冷板的方案是最接近真实情况,不过通过一系列的工况表明,铜块方案同样可以获得接近真实的Rjc数据,且相比冷板方案更加简单快速。
|
方案 |
Lid上表面温度 |
结温Tj |
壳温Tc |
结壳热阻Rjc |
|
定温 |
定值20℃ |
20.351 |
20 |
0.117 |
|
冷板 |
变化 |
21.712 |
21.422 |
0.097 |
|
铜块 |
变化 |
20.839 |
20.537 |
0.101 |
表1.Rjc数据
4.2 TIM的材料属性
除了上一节讨论的边界条件以外,TIM的材料属性同样非常重要且难以确定。通常的确定TIM有效导热系数的方法,是制作多个涂有不同厚度TIM的测试样品,通过测定样品的温度,可以得到导热性跟厚度的函数关系。该方法存在的问题是,由于测试数据的波动,导致很难拟合出热阻跟厚度的准确线性关系,且需要很多样品。
在我们这个案例中,TIM的厚度不能超过50 μm。所有TIM的厚度都控制在38μm左右,没有其他厚度的TIM来拟合该函数关系。因此,我们必须通过单一厚度的TIM来确定其导热系数。
.png)
图10.确定TIM有效导热系数的流程图
为达到此目的,我们设计了如图10所示的流程。首先,假设一个TIM的导热系数,通过仿真得出设备的Rjc,然后与测试所得Rjc对比。若差值(△)大于既定残差(S),则赋予其另一个导热系数的值并重复上述步骤,直至残差达到标准。在本次案例中,我们发现TIM的导热系数与供应商提供的数值并不相同。
以上提供了一种获取TIM导热系数的方法。需要说明的是,该方法是基于三维稳态热仿真,即不关注封装器件瞬态热特性。此过程中功率密度假设是均匀的,由此获取的Rjc数据在某些工业应用中已经足够精确了,不过从根本上讲该方法不符合采用瞬态方法的JEDEC 51-14标准。理论上,使用瞬态方法能提供更为详细的封装器件热特性。因此,在第5节中,我们将讨论瞬态方法。
4.3 Rjc测试
使用第3节提到的试验装置,我们得到如图11所示的测试结果—结构函数。在冷板和散热片之间涂上两种不同的导热材料,一种导热性好,一种导热性差。就Rjc来说,差距非常小不到0.2 K/W,两条曲线看起来彼此非常接近且分离点不清晰。
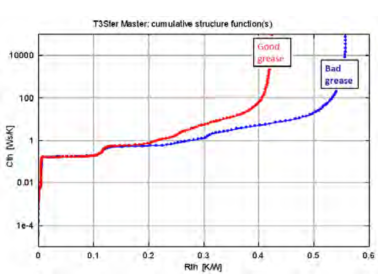
图11.结构函数图
为此,我们画出结构函数差值曲线,如图12所示。
.png)
图12.结构函数差值曲线
该点的Rjc是0.113 K/W。在实际的测试过程中,通常会测量多次取平均值,本例中该平均值是0.11 K/W。我们的数据显示不同次之间的测量结果差别非常小,由此也证明测试设备的准确性很高。
接上篇
5. 瞬态热特性研究
本节我们讨论瞬态模拟方法并尝试尽可能详细的匹配真实测试条件。二极管的温度响应受导热系数、热容、尺寸、结构和功率影响很大,因此,以上所有因素都必需考虑在内,以便能更好的匹配试验数据。
5.1 瞬态模拟
在TIM的有效导热系数确定以后,我们可以建立一个完整的3D封装器件热模型来执行瞬态模拟。如图13所示,该模型尽可能详细的把结构考虑进去。包括焊接凸点(solder bumps),加热电阻(heating resistors),底部填充层(underfill),衬底层(substrate layers),焊球(solder balls),PCB布线,尼龙块(Nylon block),环氧树脂封装材料,功率分布和二极管的位置信息。
理论上讲,若运行稳态仿真,得到的Rjc应该跟前一节提到的相同。但是要想知道详细的结构信息,则需要进行瞬态热特性研究,因为这些详细的特征会影响到二极管的温度响应。图13a是带焊接凸点(solder bumps)和底部填充层(underfill)的硅芯片的底部视图;图13b是芯片固定在衬底(substrate)上的顶部视图,仿真时会考虑所有的衬底结构层(substrate layers);图13c是封装器件直接通过焊球(solder balls)安装在PCB板上;图13d所示是整个组件,芯片一面贴在冷板上,中间涂上导热胶以改善接触。顶部压一个尼龙块来控制导热胶的厚度。
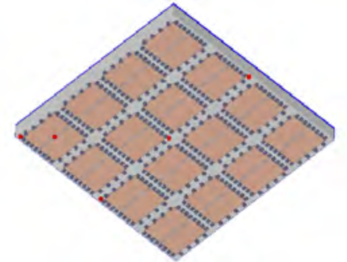
图13a 硅晶片焊盘的底部视图

图13b 硅晶片置于衬底上的顶视图

图13c 芯片安装在PCB上
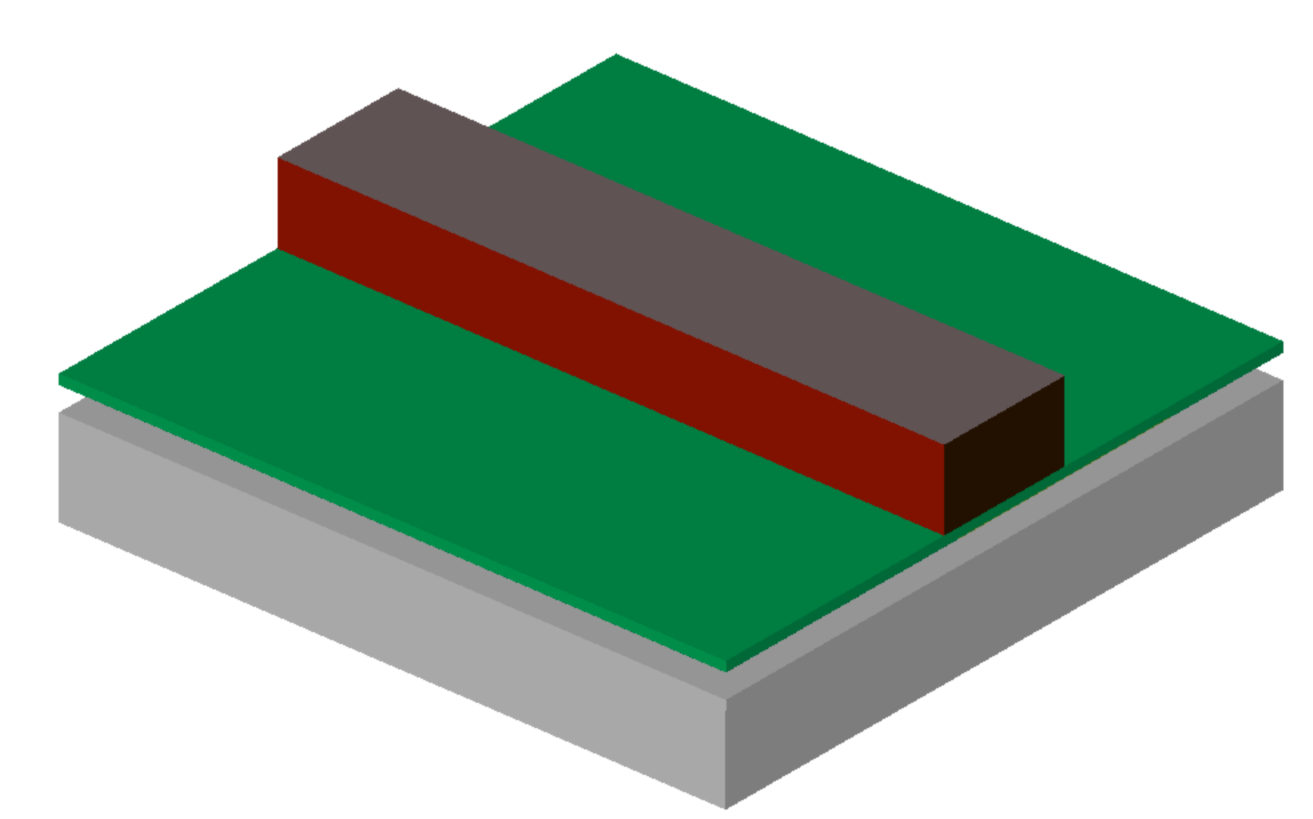
图13d 试验装置整体图
5.2 功率分布对结构函数的影响
本文中测试所得的精确的结构函数,能完全消除无论是不同供应商,还是制造工艺问题所导致的材料属性的不确定性。我们所使用到的测试硬件T3SterTM能以最快1μs的采样频率同时采集多个二极管的信号数据。除了材料属性和结构之外,功率分布也是影响结构函数的重要因素。在本节中,我们采用的热测试芯片包含16个加热单元,10个二极管传感器在上面。如图14所示,每个单元包含一对加热电阻。
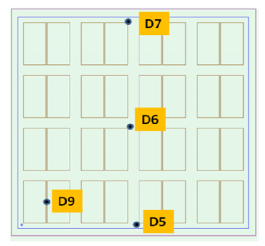
图 14 二极管传感器的位置
我们选中图中编号5,6,7和9的传感器,因为他们的位置非常具有代表性。D6位于芯片的中心位置,测试的是结温Tj,用于计算Rjc;D5和D7处于芯片的边缘位置;而D9位于左下角单元的中心位置,也恰好是一对加热电阻的中间。此外,D5、D7和D9与它们各自所对应的加热电阻的距离也相等。
以上4个传感器所测得的瞬态温度响应曲线如图15a所示,显示了不同位置温度响应的差异。我们以初始温度相同将曲线做偏移处理,如图15b所示,我们便可以轻松的对比各传感器的响应速率。可以看出,位于加热电阻之间的D9响应时间最短,大约先于其他传感器400μs;D5和D7由于他们与加热电阻的距离相等,所以它们的温度响应曲线基本相同;D6和D9温降幅度相同但是降温过程不太一样,这是由于二极管从内到外传导过程中经历的结构的热容不同造成的。
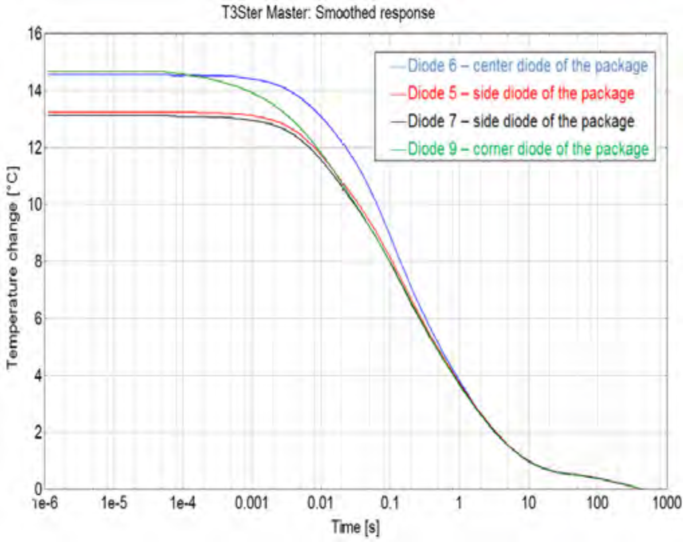
(15a)无偏移的温度响应曲线
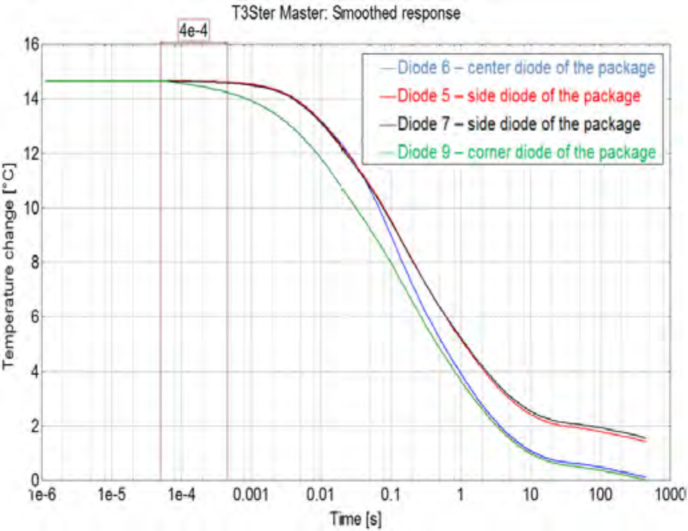
(15b)偏移后的温度响应曲线
总的来说,造成温度响应曲线差异或者传播延迟的原因有如下两个:1. 二极管传感器跟加热电阻之间的相对距离不同,这是与热源的热容相关的2.由于器件的结构和材料的不同,每个二极管热传导路径上的热容不同。之所以选择D9作为下一节仿真结构函数与实验结构函数校准的对象,是因为D9最接近加热电阻,延迟最短。对于有多个二极管且跟加热器距离不相同的设备,我们推荐采用相似的二极管来进行结构分析和模型校准。
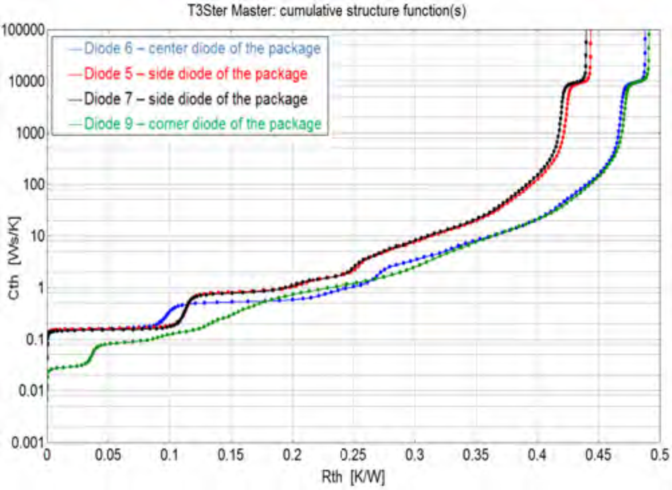
图16 实验结构函数曲线
当前有许多潜在工程应用需要关注到功率分布对结构函数的影响分析,也正是本人在研究的一个方向。其中一个例子就是掌上移动终端,基于时间的温度响应函数对其甚为重要;另一个典型领域就是多芯片或多核处理器,因为基于温度响应的功率分布会影响到它的电学性能。详细掌握功率、温度和时间之间的关系,是下一代IC设计和制造的重中之重。
5.3 校准仿真结构函数(通过实验
数据得到的结构函数)
前面的章节我们讨论的温度响应曲线和结构函数均来自于实验。在这一节里,我们尝试运行三维瞬态仿真来获取D6的温度响应,曲线通过处理、构造,最终转化为“仿真结构函数”。与经典热模拟一样,仿真结构函数跟实验结构函数匹配的不是很好。造成差异的原因主要有:不确定的材料属性、细小特征的仿真难度、或者不准确的功率分布定义等等。现在的好消息是,我们可以通过实验结构函数来校准仿真结构函数了。
首先,运行三维封装器件热瞬态仿真,将温度响应曲线的结果导入T3SterMaster来建立初始仿真结构函数;第二步,通过对3D热模型做些改变并重新生成结构函数;第三步,将新生成的结构函数与实验结构函数进行对比。在多次修正3D热模型和迭代以后,最后生成的仿真结构函数会与实验结构函数匹配的非常好。这一校准过程的重点,是明确3D热模型中具体哪个参数需要改变来匹配结构函数。在本次研究中,我们选取硅芯片上的热源尺寸和TIM以及导热胶的热阻来作为调整变量,以期得到与实验结果匹配的仿真模型。
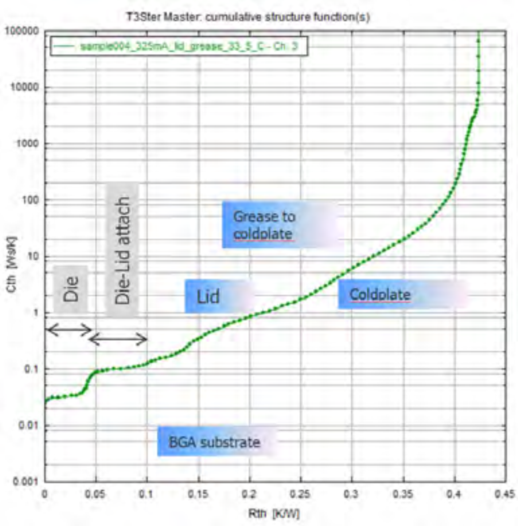
图17 积分形式的初始仿真结构函数
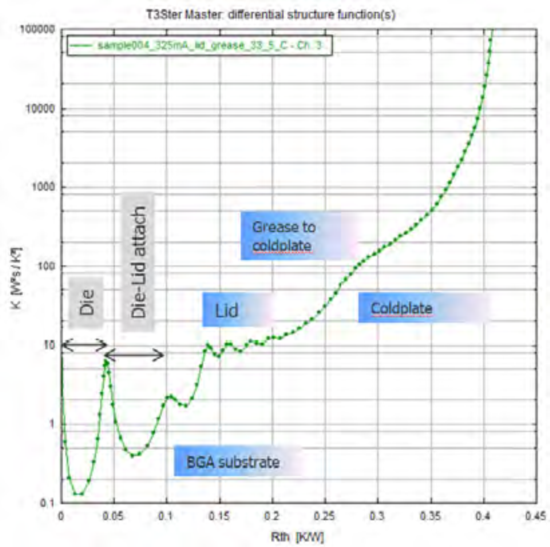
图18 微分形式的初始仿真结构函数
图17和图18展示了初始仿真结构函数的积分形式和微分形式。从图19可以看出初始仿真结构函数与实验结果函数存在较大差异,大约有30%~40%,造成此差异的因素有很多,前面的章节已经提到过了。如果需要做到高精度的预测,特别是对于系统级热解决方案而言,就必须消除仿真和实验之间的误差。
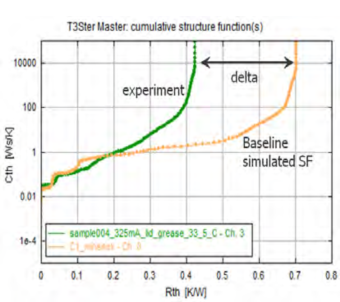
图19 实验结构函数&初始仿真结构函数
我们从芯片区域开始校准,然后逐渐向外改变其他参数来促使仿真结构函数与实验结构函数相匹配。如图20所示,改变发热区的形状和尺寸,并且模型明确地考虑了所有的焊接凸点(solder bumps)和底部填充(underfill)结构。
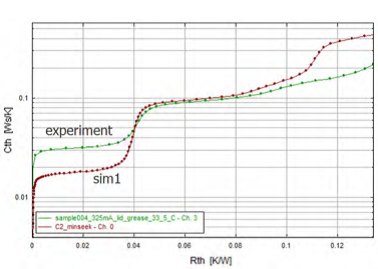
图20.die region附近区域的试验结构函数和初始仿真结构函数
图21是通过更换热阻更高的TIM材料来校准模型。图22是通过在冷板和封盖之间涂上热阻更低的导热胶。
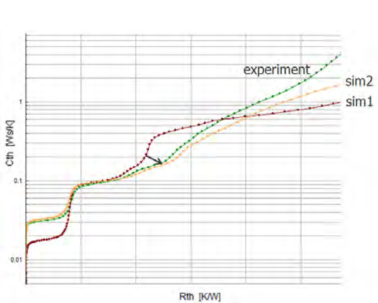
图21.实验结构函数和校准仿真结构函数
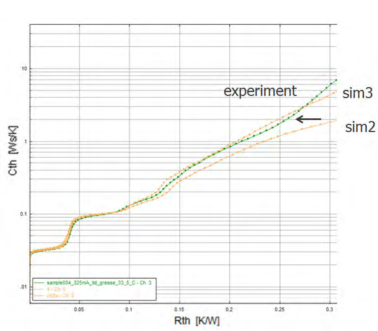
图22.实验结构函数和校准仿真结构函数
图23是最后通过多次迭代后校准好的结构函数,可以看到在热阻为0.3~0.4 K/W区间内曲线不匹配。这是由于该区间表征的是冷板散热效果的好坏,并不属于封装器件关注的范畴。因此,校准到此为止。经过校准的仿真结构函数,精确的反映了封装器件从二极管到冷板之间的真实热阻。
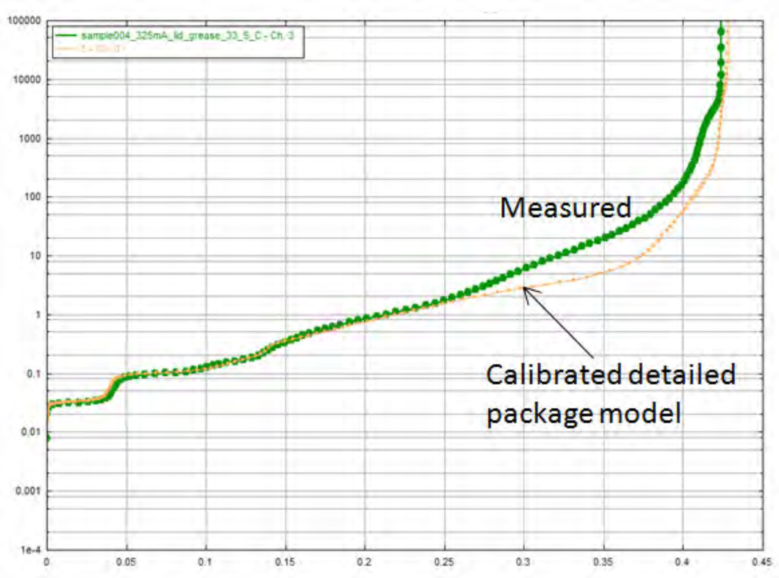
图23 实验结构函数和最终校准好的仿真结构函数
6. 强制对流Rja测试
Rja(结到环境的热阻)是最终成型产品中一个非常重要的热参数。我们通过在封装器件上安装一个强迫对流冷却的散热器来评估其散热效果,如图24所示。通过4个螺丝(图中看不见)将散热器架固定在PCB板上,通过调节风扇转速来改变空气流速,进而研究Rja的变化。风扇转速通过外加电压来控制。

图24.强制对流冷却
图25展示了一组Rja的测试数据。外加电压越高,风扇转速越高,所以Rja的最小值是0.755 K/W。10 V和8 V电压对应的Rja分别是0.775 K/W和0.793 K/W。
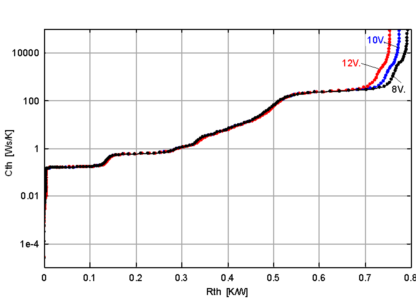
图25.不同驱动电压下的Rja测量值
7. 结论和后续工作
综上,本文展示了如下工作和能力:
a. Rjc的仿真和测试;
b. Rja的测试;
c. 设备的瞬态热响应;
d. 生成Delphi模型的过程。
我们将继续在如下方面展开进一步的研究:
a. 制定能更好的评估几何结构和材料属性对Rjc标准的影响的仿真计划;
b. 实现生成Delphi模型结构函数的自动化;
c. 更多的封装器件瞬态行为;
d. 改善多芯片和多处理器封装器件的测试计划。








 沪公网安备 31010602003953号
沪公网安备 31010602003953号