固态功率组件热耦合效应研究
日期：2012-06-19
杨双根
(中国电子科技集团公司第三十八研究所，合肥 230031)
摘要： 本文基于热叠加原理论研究了固态功率组件中多个离散分布的集中热源的热耦合效应，并证明强迫对流下应用热叠加原理计算的温度场与整场系统数值模拟的结果相当吻合，用它来进行热耦合效应的分析研究是有效的。
关键词：绝热传热系数；叠加核心函数；热叠加原理；热耦合
中图分类号:ＴＮ830.5 文献标识码: A
The Research for Thermal Conjunction Effect of Solid Power Modules
YANG Shuang-gen.
( CETC No.38 Research Institute，Hefei 230031,China)
Abstract: The thermal superposition Principle is put forward for the research of discrete heat sources’ temperature field and thermal conjunction effects。In forced convective cooling，fine agreement exists between the result of system numerical simulation and the result based on thermal superposition Principle.，and using thermal superposition Principle for The research of Thermal conjunction is an effective method。
Key words: adiabatic heat transfer coefficient；superposition Kernel function；thermal superposition Principle；
1 引言
固态化技术是雷达领域研究的重要课题，各国都在竞相开发出先进的全固态雷达和相控阵雷达。军事需求以及电子技术的迅猛发展，使得固态功率器件和设备日趋小型化发展，功率密度不断提高。器件的许多故障机理都与器件过热相关，因此，在器件内部保持较低的且均匀分布的结温是非常重要的。由于热控制措施不合理造成的热失效问题变得越来越突出，散热问题已成为先进电子元件应用的一个主要制约因素。
雷达发射机功率组件一般由多个功率晶体管组成，组件的热设计直接影响雷达发射机的性能指标和系统的可靠性。多个集中式热源离散分布在散热冷板上，理想的热设计能够使每个热源的热沿着最短的传热途径流向热沉而使热源相互间
的热耦合趋于零，但这是不现实的，因为实际应用中需要有效增大散热面积，依靠热扩展体把集中式热源的热量有效扩展，所以热源相互之间会产生热耦合现象，只不过根据其热通路的长短，有的相互影响比较大，有的相互影响则很小。随着计算机技术和计算流体动力学（CFD）技术的不断发展，传热学数值模拟技术发展很快。利用传热学数值模拟技术基于热叠加原理来研究功率设备温度场的热耦合效应是一种很好的方法。
2 热叠加原理
热叠加原理意味着：热源的热效应是线性的，利用线性叠加理论，由求解一些互不约束的热源所产生的温度场能得出整个系统（指由这些互不约束的热源所组成的系统）的温度场结果。热叠加原理是在绝热传热系数和叠加核心函数这两个概念基础上建立的。
必须指出在换热模型中任何非线性的因素，如，辐射换热及浮升力影响均会产生与预期结果的偏差。对强迫对流的系统，这个原则在很广的范围内都是适应的，因为在强迫对流时，浮升力影响很小。
热源布局的复杂多样，难以以公式的形式定量地给出热源相互之间的耦合传热影响因子关系式，但可以采用CFD方法，用如上的热叠加原理对热源的热效应展开研究。
2.1 绝热传热系数
Moffat[3]提出了一个适合在计算流体动力学中使用的绝热传热系数
的概念，其计算步骤如下：
的概念，其计算步骤如下：
1) 当元器件没有施加功率
时，而且没有热传导或热辐射等，这个元器件将在
下工作，即围绕器件周围空气的平均温度；
时，而且没有热传导或热辐射等，这个元器件将在下工作，即围绕器件周围空气的平均温度；
2) 当施加热耗
到元器件上时，将会产生平均表面温度
；
到元器件上时，将会产生平均表面温度；
3) 由
求得
，
仅仅与流场有关。
求得，仅仅与流场有关。
用CFD求解流动和传热问题时，计算出来的绝热传热系数能直接应用。
2.2 叠加核心函数
在一个传热系统的求解区域里，感兴趣的点经常是工作温度条件最恶劣的点，如每个
器件的结温（壳温）或者对温度比较敏感的点。
基于如上2.1的绝热传热系数的理论，热叠加核心函数，见如下公式(3),按下列步骤得出：
1） 建立计算模型，将模型中所有的热源热耗属性失效，即在热分析中使之不起作用。
2） 依次施加单位热耗到每个热源，并且激活，计算收敛后，系统里任何一个感兴趣监测点的温度值逐一被储存,这些点的值以矩阵的形式表示出来。当有多个离散热源时，这个过程被重复多次。因为第一次流动问题的求解已经收敛，所以后面的计算不会占用太长的时间，每次也仅仅重新计算温度场。
3） 确切知道每个元器件的热耗之后，通过矩阵运算，即可以求出系统里感兴趣点真正的温度值。
假定有n个集中式热源离散分布于散热基板上，其中m个感兴趣的局部最高温度需要有效地监测，如下一个矩阵被建立，姑且称之为热影响矩阵，它将n个热源与m个监测点的温升值有效地联系起来，矩阵项元素包含着监测点温度与局部环境的温升，即：
因为是单位热耗（1W）下的温差，可以按如下的矩阵理解，即：
（1）
（1）
的量纲与热阻相同，当
时，
可以理解为热源
自身产生的热阻效应，当
时，
可以理解为热源
对热源
所产生的耦合热阻。
一旦每个热源的热耗都已知，即
已知时，则：一个矩阵乘法运算然后被执行，产生的m维矩阵矢量代表着每个检测点与工作环境的温升，即：
已知时，则：一个矩阵乘法运算然后被执行，产生的m维矩阵矢量代表着每个检测点与工作环境的温升，即：
（2）
（3）
而且，这个矩阵亦能和工作环境温度相叠加，得出每个监测点真正的温度。
由以上计算过程可以看出，热叠加原理至少可以用于两大类问题的分析和求解上。
第一、 对CFD方法提出了一个有效地补充，有时候元器件真正的散热功率有时很难准确得到，而在此之前也可以就给定的资料（如器件和电路布局）进行CFD分析，一旦实际工况确定（如：各个热源热耗已知了），通过简单的矩阵运算即可计算出其实际工况下的工作温度；
第二、可以有效地分析热源之间的热耦合效应，即元器件自身的热效应和受其它元器件的耦合热效应。
3 固态功率组件的热耦合效应研究
下文以某固态功率组件为例，来分析温度场的叠加和热源相互间的热耦合效应。
某固态组件有13个热源，分别命名为s1～s13，在散热基板上各个热源的中心位置均设置监控点，则将会产生一个13x13的热影响矩阵。
建立了较为精确的三维CFD模型，如图1所示。湍流模型采用了LVEL
模型，近壁区采用壁面函数法，网格采用块结构化网格技术，流场计算中采用基于交错网格的SIMPLER算法，对流项采用了QUICK格式离散，采用Flotherm solver求解。
模型，近壁区采用壁面函数法，网格采用块结构化网格技术，流场计算中采用基于交错网格的SIMPLER算法，对流项采用了QUICK格式离散，采用Flotherm solver求解。
在数值模拟中，做如下假设：
（1） 流体满足Boussinesq假设；
（2） 流体及固体物性参数为常数；
（3） 流体在壁面处无滑移；
（4） 流动是定常的；
（5） 不计自然对流和辐射换热的影响。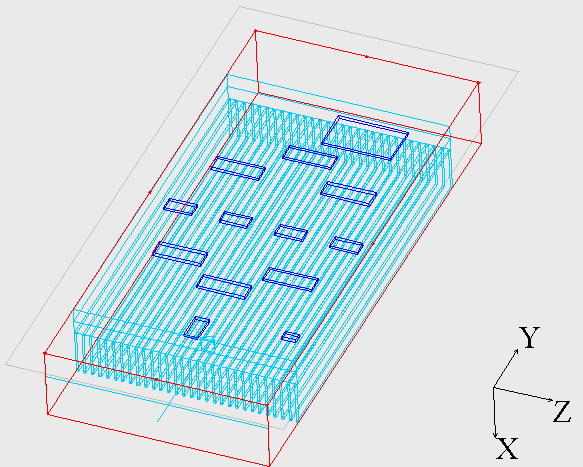
图1 三维CFD计算模型
通过如上的步骤，计算得出热影响矩阵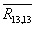
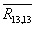如下：
如下：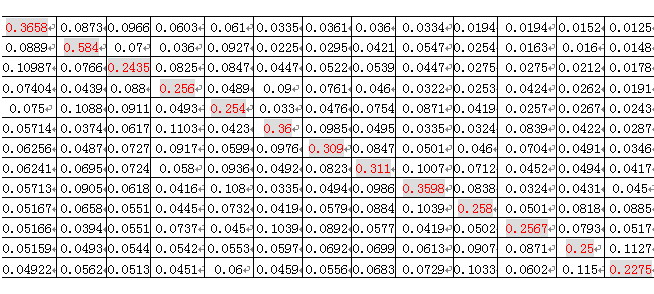
在如上矩阵中，对角线中的数值
可以看成是第
个热源自身热耗和温度差产生的热阻,而
可以看成是第
个热源对
热源的耦合热阻。
可以看成是第个热源自身热耗和温度差产生的热阻,而可以看成是第个热源对热源的耦合热阻。
已知13个热源组成的热耗矩阵如下：
（4）
（5）
求得的各个监测点与周围流体的温升矩阵如下
（5-5）
由热叠加计算过程和结果，分析得出如下结论：
* 热源之间的温度场相互耦合；
* 热源自身引起的热阻最大，耦合热阻和热耦合路径的长短有关；
* 热耗和热阻决定了温升，热源自身引起的热阻大，但若自身的热耗小，周边高热耗热源会对其产生一个更高的耦合温升。
利用CFD模型做整场系统分析的温度场如图2所示。
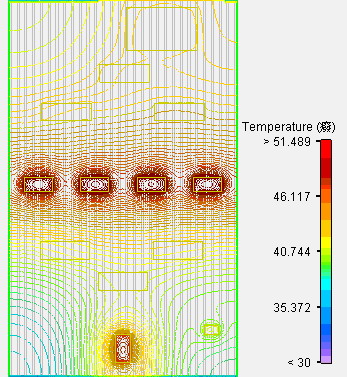
图2 整场系统数值模拟的温度场
将叠加后的结果与整场系统数值模拟的结果相比较，见图3；分析得出各个监测点的相对误差如表1所示。
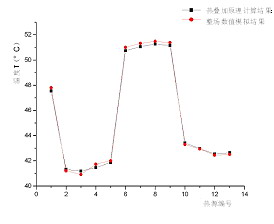
图3 热叠加原理计算与整场数值模拟结果比较
表1 监测点与环境温升相对误差(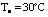 
)
)|
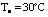温度监测点
|
系统模拟温度
|
热叠加后的温度
|
与环境温升的相对误差
|
|
S1
|
47.80
|
47.55
|
1.4%
|
|
S2
|
41.22
|
41.33
|
-1%
|
|
S3
|
40.93
|
41.20
|
-2.5%
|
|
S4
|
41.74
|
41.48
|
2.21%
|
|
S5
|
42.00
|
41.86
|
1.17%
|
|
S6
|
51.00
|
50.74
|
1.24%
|
|
S7
|
51.32
|
51.06
|
1.22%
|
|
S8
|
51.48
|
51.26
|
1.02%
|
|
S9
|
51.38
|
51.15
|
1.08%
|
|
S10
|
43.29
|
43.42
|
-1%
|
|
S11
|
42.94
|
42.97
|
-0. 2%
|
|
S12
|
42.45
|
42.55
|
-0.08%
|
|
S13
|
42.51
|
42.64
|
-1%
|
4 结论
本文对13个热源、13个监测点应用热叠加原则计算得出的温升值和系统模拟结果相比较后分析出其相对误差绝对值
，证明强迫对流下应用温度场叠加原则计算的温度场与系统的温度场结果是相当吻合的，用它来进行热耦合效应的分析研究也是十分有效的。
，证明强迫对流下应用温度场叠加原则计算的温度场与系统的温度场结果是相当吻合的，用它来进行热耦合效应的分析研究也是十分有效的。
参考文献
[1]国防科工委军用标准化中心全国军事装备可靠性标准化技术委员会. 电子设备可靠性热设计手册实施指南[S],1992.
[2]陶文铨.数值传热学.西安:西安交通大学出版社,1998.
[3]Moffat.R.J, Getting the most out of your CFD program,
8th intersociety conference on Thermal and Thermomechanical Phenomena in Electronic systems(ITHERM).PP.9-14，San Diego，CA. May 2002.
沪公网安备 31010602003953号