—确保车载发射机不危及车辆安全是十分必要的

文章来源：《电磁干扰与兼容》2007年春季版www.interferencetechnology.com.cn

目前，越来越多的车载天线广泛地应用于各种车辆。在获得令人满意的通讯性能的同时，确保车载发射机造成的系统内部或系统间的电磁兼容问题不危及乘车者和公众的安全也很有必要。

在原形成型之前的基本系统设计构思中，要评估已装天线的性能特征和可能的电磁兼容危害与车载发射装置的关联性，因为在设计周期的早期阶段实施改变要简单、经济得多。此外，车辆环境的谐振特性会导致其内部产生较大的空间场变化，而由于车辆的几何复杂性，场传感器不容易接近许多部位。因此实验测定性能很大程度上受到实际条件的限制。只有做出相关硬件，实验才能得以实施，但是这样成本高、耗时长，还有可能达不到预想的所有效果。

整车电磁仿真是解决该问题的可行性方案，它也为摆脱实验方法的局限、实现这样的数据分析提供了可能性。但是在我们自信地运用该模型之前，有必要确定计算结果的可靠性。本文略述了对于安装在车顶后部或挡泥板后部的单级天线电场模型验证数据的研究。虽然我们对于车辆外部和内部场分布的研究同样感兴趣，但外部场的测量比内部场的测量具有更大的可行性。不过内部区域和外部区域透过车窗缝隙密切相连，因此对车辆外部的近场验证将为内场分布预测提供可靠的依据。

车辆仿真与测量

这里所述的仿真由MIRA电气公司实施，而测量则由另一个机构(英国，QinetiQ)通过使用与仿真中相同型号的车辆来完成。尽管测量和仿真最初是各自独立进行的，但随后由MIRA公司对两套数据进行了比较分析以达到验证的目的。

车辆仿真采用全波TLM(传输线矩阵)和三维场建模技术，该技术是建立在来源于车辆CAD数据的模型基础上的。一般说来，TLM被认为是一种时域技术，它适用于获得电磁兼容应用所需的宽频结果（一般大于或等于1GHz ）。但是在此应用中，我们关心的频段受到发射机频率（大约400MHz）的限制。尽管如此，TLM对于模拟像车辆这样的复杂结构仍不失为一种很好的选择，因为它通常是一种基于矩形单元的网状结构。与非结构、基于表面的结构如边界元法（矩量法和有限元法）相比，直角网格的优势在于它相对来说节省存储所需空间。因此，使用TLM模型，包括需要描述外部散射和内部谐振的车辆的内外表面都不会受到内存需求的影响。TLM技术与大家所熟知的FDTD（有限差分时域）法有些相似，由于这些原因，这种方法被广泛地运用于电磁兼容模型中。TLM模型和FDTD模型的主要缺点是因为直角网格结构需要用梯形来描述曲面，这样会影响精度；但在许多实际应用中，这种近似值方法是可以接受的。

车辆的几何结构用分级网格来进行离散，以减小计算量，同时确保在所研究的频点获得可靠传播并建立一个令人满意的可代表车辆几何特点和预期场梯度的结构。在这种情况下，车辆的几何结构分成每边2.5 cm的立方单元网格，而外部区域的网格尺度增大到5cm。后者提供了这项研究中对于所研究的频点而言为足够的离散化。模型构造仅限于主要的金属部件，因为，以前的实验研究表明，其它材料的部件对1GHz以下内部场耦合影响很小。

为使这个模型完整，在研究中（模拟简单的细线天线安装在后车顶或后挡泥板）用天线的描述既丰富了基本的车辆几何结构，也增加了车辆的电磁有效特征，如车窗加热器。图1给出了这样一个模型的例子：这个插图还包括了“人的模拟”，用这个车辆模型可以评估乘车者的场辐射问题，尽管本文描述的是一种空车状态。

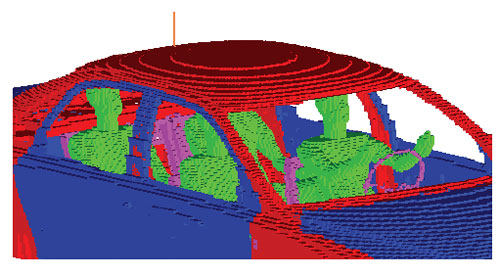
图1. 安装了车顶天线和后窗加热器、集成了乘客模型的TLM车辆模型例子

我们计算了环绕车辆和周围空间的电场和磁场强度（远达10m的距离），提取了垂直空间中高度为0.5m、1m、1.5m和2m的电场计算结果。计算数据被规格化成与测量相同的功率水平，以便与实验数据相比较。

这个测量中使用了一个机器手臂在车辆周围的规则网格放置等方向的场探针，来采样车载天线在不同水平面上产生的电场分布。测量是在室内进行的，对于场测量来说，估计的不确定度为±3 dB。在一个9m长、6m宽的区域内，数据点的间隔是25cm，在水平面高度为0.5m、1m、1.5m和2m情况下获取数据。

应该注意的是，虽然在测量中天线的位置与仿真的情况相类似，但他们不完全一样。仿真的车顶和挡泥板的天线比测量的靠前6.25cm，而且安装在挡泥板的天线在横向上也有15.25cm的不一致。这些不同是因为测量和仿真任务是各自独立进行而引起的，并且在任务完成后，只是仅仅将数据汇总在一起。

二维场分布的定性比较

对于诸如某一点的频率响应或沿着一维路径的场分布这样的一维参数来说，在图中同时画出两个（或多个）结果进行比较是很容易的事情。在将模型数据与测量值相比较时，通过画出基于不确定度的测量值上下限来显示不确定度的幅值是可能的。这个方法给出了测量和计算结果关联程度的直观印象，其中包括测量结果中不确定度的影响（在仿真中估计不确定度的方法是今后进一步研究的课题）。例如，在图2中显示出了在这个场合的电场测量中不确定度的显著性，这个图是一个安装了车顶天线、水平面1m高度情况下二维数据的纵切面图。

图2中显示的片段表明，所有的计算数据都在估计的测量范围内，只有虚线在测试范围的中间区域超过测量值的上限。对于测量和仿真数据的匹配来说，这个结果看上去是非常令人满意的。可惜，这种简单的认识不足以完成我们这里全部二维数据的研究。

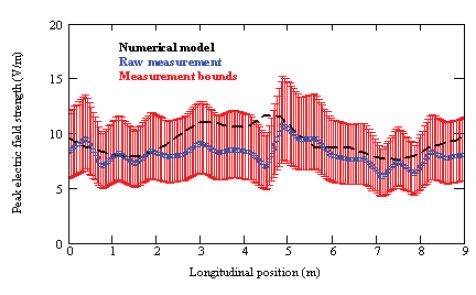
图2. 包含不确定度的一维计算和测量数据

通过从计算结果和测量不确定度，估算出的最接近可能的测量值，可以得出一个类似于图2的比较结果，能够反映测量不确定度。对于二维情况，每次测量的上限(Ujk)和下限(Ljk)与计算结果(Cjk)的比较推导出调整过的测量数据(Ajk)，由下面的式子决定：

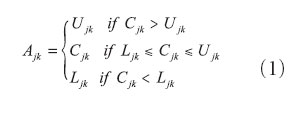
图3画出了这个过程的简单的一维数据，它显示出调整后的测量数据和计算数据以及原始数据之间的关系。

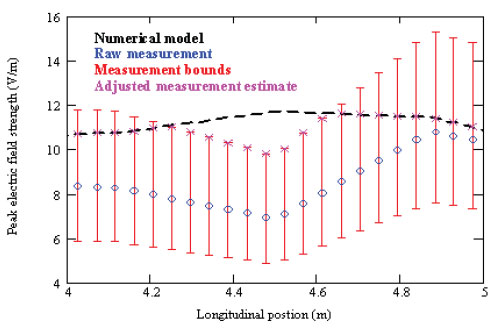
图3. 一维计算和测量数据，以及反映测量不确定度的已调整数据

（下一部分）